What are binary numbers?

WORK IN PROGRESS!

This page is not quite ready for visitors yet. Please check again another time.

Okay, so now this wild ride through computing is going to take a hard turn towards the mathematical. But don't worry, you're strapped in and perfectly safe. This book is fitted with airbags.

The topic at hand is this: if digital electronics only lets us use 1s and 0s, how on earth can we represent more complicated things like big numbers, alphabetical characters, YouTube videos or tweets by Dean Norris?

To find out the answer to this question, we might first want to consider how the regular numbers that we all know and love work.

What are decimal numbers anyway?

When I was a young rosy-cheeked scamp of a schoolboy, sometime astonishingly close to when Sega Master Systems were first hitting the shelves, we used to have these purple plastic bricks to help us learn numbers. They were, or at least are now, called 'base ten' blocks, and there were four different types: units, which were little cubes of roughly perfect choking size for a small child; tens, which were like a line of ten units in a row; hundreds, which was a 10x10 flat plastic square; and thousands, which was a hefty sized cube maybe half the size of a house brick and, frankly, just as dangerous when used as a weapon.

TODO PIC

Armed with a mere nine of each of each of these four different types of block (i.e. thirty six in total), it was actually possible to represent any number between 0 and 9,999 (which I'm sure was a number far too big to expect any pre-pubescent to be able to deal with back then).

How is this numerical feat possible? Well, it's all to do with the system we use to represent numbers, and it turns out there are lots of ways representing numbers can be done. Remember the Romans? Of course you don't. Perhaps the reason their empire collapsed is because of the daft way they represented numbers. In Roman numerals, if I want to write the number 1985 then I have to write MCMLXXXV. Fair enough, looks like you need twice as many characters to represent our of "our" numbers in Roman numerals, right? Wrong. Let's take two more interesting examples: 999 is CMXCIX in Roman numerals; and 1000? Well that's just M of course! Don't ask me to explain why, because it would be a waste of both of our times. The important thing to remember is that it's completely bananas.

To be fair, Roman numerals were invented a bloody long time ago. The number system most of us use today is properly called the Arabic (or Hindu-Arabic) system, although there are other less common names for it. A lazy skim of Wikipedia tells us that it was first seen in around the 9th century AD and imported to Europe in roughly the 10th century. Essentially what the Arabic numeral system gives us is nine symbols, namely the digits from 0 to 9. Of these nine, the most cunning by far is the innovative number 0, which was actually invented in India quite a lot earlier that the Arabic numerals.

How we choose to use these nine numerals depends on what base or radix we're working in. Remember those 'base ten' blocks? So-called because the base we're working in there is base ten, or decimal (or sometimes denary). How do we write base ten numbers in Arabic numerals? The 'base ten' blocks show us how:

1. Count up in units until we have either finished counting to the number we wish to represent, or we have counted out nine units.
2. If we haven't yet reached the number we wish to represent, increase the number of tens we have by one and get rid of the nine units.
3. Repeat steps 1 and 2 until we have either reached our number, or we have counted nine tens.
4. If we haven't yet reached our number, this time increase the number of hundreds by one, and get rid of the nine tens and the nine units.
5. Repeat steps 1 to 4 until we have either reached our number, or we have counted nine hundreds.
6. ...

Of course, we repeat for thousands, tens of thousands, hundreds of thousands, millions, etc. etc.

When we have finally reached the number we wanted to represent, we look down at the tally of thousands, hundreds, tens and units we have collected and lo and behold we wrote a number.

In this process, it's a bit like each pile of hundreds, tens and units, etc. was a column which can contain no more than nine. Every time nine is reached it goes back to zero and the next column to the left goes up by one.

But why do our columns have those particular numbers? Why is it hundreds, tens and units; rather than, say, sixties, twenty-sevens and fives? Units is fairly easy to explain: if we didn't count up by one each time, we'd miss some numbers and then we'd be in some serious trouble, so our right hand column must count up by one every time. But what about the tens column? Why ten? Well, it turns out that the choice of ten is completely arbitrary. The best guess is that our system used ten for the second column because most of us have ten fingers on our hands. But it's the arbitrary choice of ten which determines how many symbols we need, not the other way around. So the Arabic numerals go from 0 to 9 because someone decided to use ten as the unit of the second column! In fact, it's from that number that we take the name of the base. The second column counts ten units, so we need ten symbols and so we must be working in base ten. The maximum number that the units column can contain in base ten is the highest symbol value, which is 9 – one less than the base number.

Now what about that third column, the hundreds? Well, that works in the same way as the tens column, except instead of counting units it counts tens. So each hundred is worth ten tens. Thousands are worth ten hundreds, or ten tens of tens. It's all starting to make some vague sense!

Mathematically, we can say that a four digit number, $n$, written in base ten using Arabic numerals is the following sum:

$$n = 10^3\theta + 10^2h + 10^1t + 10^0u$$

where $u$ means the number of units, $t$ means the number of tens, $h$ means the number of hundreds and $\theta$ (the Greek letter theta) means the number of thousands (since we've already used $t$ to mean tens).

Notice we're using the exponent operator here. We remember that $10^2$ means $10\times10$, and that $10^3$ means $10\times10\times10$. But what about $10^1$ and $10^0$? Well $10^1$ is pretty easy, that is just $10$. But $10^0$ is a little counter-intuitive. Turns out that any number raised to the power of 0 is always 1 or, in maths speak, $b^0 = 1$ for any number $b$.

Of course, we don't need to stop at thousands, we can go past tens of thousands and hundreds of thousands on through millions to an infinity of columns, all of which are powers of ten. Let's imagine we've got $N$ columns, and that we are going to call each column $c_i$, with $c_0$ being our right hand column, $c_1$ being the second (tens) column, etc.

$$n = \sum_{i=0}^{N}10^i c_i$$

This is a wonderfully neat and compact way of describing any decimal number representation.

If your eyes are starting to glaze over at this point, take heart, we're done with equations. Don't worry too much if you didn't follow all of that, the really important thing is that you can count in hundreds, tens and units like back in school.

But things are going to get super weird now. Now that we know how decimal numbers works, it's time to take a deep breath and dive into the exotic world of other number bases.

What if we only had one finger?

Imagine that you were born on some distant planet, in a galaxy far, far away. Let's call it "planet Binar". Now imagine that the sentient lifeform on planet Binar only have two finger. Maybe they have two arms, each with a single finger at the end; or maybe they have one arm with two fingers. It doesn't much matter. We might imagine that without a compelling reason to count up in tens like we do, perhaps they'd only count up "in twos". But this is madness! How would counting in twos work?

Well, let's start by remembering that in our base ten system, we have ten symbols: the numbers from 0 to 9. Okay, so if we only have two fingers perhaps we can only imagine two symbols: 0 and 1. The 0 symbol is essentially the absence of fingers, and the 1 symbol we use when we are holding up one of our fingers. What about if we hold up all of our fingers? On planet Earth we say that's 10, in other words when we have all our fingers held up we use our second column. Doing the same on Binar would result in the same representation – 10, but on Binar we would only have counted to Earth's number two in order to use the second column.

Let's repeat that, because it's super confusing:

• On Earth, because we have ten fingers, we count like: $0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10$.
• On Binar, because we have two fingers, we count like: $0, 1, 10$.

The 10 on Binar looks just like our number ten, but it isn't. It's actually our number two. Why? Because we got to it after counting up twice from zero!

tip

Conventionally when counting in decimal we say the word "ten" for the number 10, but in other number bases (and indeed on planet Binar) we would say 10 as "one zero". Trust me, it's much less confusing that way.

If your brain isn't oozing out of your ears by this point, congratulations. But there's more to come, so perhaps grab some ear muffs, because what happens after 10 on Binar? Well, consider that on Earth once we get past ten we start all over again from 0 to 9 in the units column. The people of Binar can do the same, except they still only have two fingers and so it's not very long until we've got to the end again:

• On Earth, because we have ten fingers, we count like: $10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20$.
• On Binar, because we have two fingers, we count like: $10, 11, 100$.

By the time we're writing 100 on Binar, we've only counted four numbers, so 100 on Binar is equivalent to Earth's number four.

tip

Again, we would say "one zero zero" for 100 on Binar, so we don't get confused with "one hundred" on Earth.

We can keep on going up like this, so after 100 we get 101, 110, 111 and then 1000 which is the eighth number and so equivalent to Earth's number eight. After that it's 1001, 1010, 1011, 1100, 1101, 1110, 1111 and then 10000 by which point we've reached the equivalent to Earth's number sixteen.

So to recap what happens every time we move into the next column on Binar:

• Binar's 1 is the same as Earth's 1
• Binar's 10 is the same as Earth's 2
• Binar's 100 is the same as Earth's 4
• Binar's 1000 is the same as Earth's 8
• and Binar's 10000 is the same as Earth's 16

Notice a pattern? Every time we move into a new column on Binar the value of number we are representing doubles. Does this make sense? Yes it does, because on Earth, where we mostly use the decimal system, whenever we move into a new column the value of our number gets multiplied by ten. On Binar it gets multiplied by two, because of the two Binarian fingers. The multiplying by ten on Earth is what leads to the powers of ten in the equations from earlier. On Binar we would use powers of two, so the Binarian equation for number representation would be like this:

$$n = \sum_{i=0}^{N}2^i c_i$$

In other words, numbers on Binar work exactly the same as numbers on Earth with one difference – we multiply each column value $c_i$ by $2^i$ instead of $10^i$.

Another way of looking at this is that on Binar the "thousands, hundreds, tens and units" are instead "eights, fours, twos and units"!

Let's take a couple practical example, and as we do so I'm going to stop saying "on Binar" because of course we're really talking about the binary – or base two – number system, which exists as much on Earth as it does on planet Binar.

Example 1

Q. What does the binary number 1000101 represent in decimal?

A. We can calculate this as follows:

$$\begin{aligned} n &= &1&\times 2^6 &~+~ &0 \times 2^5 &~+~ &0 \times 2^4 &~+~ &0 \times 2^3 &~+~ &1 \times 2^2 &~+~ &0 \times 2^1 &~+~ &1 \times 2^0\\ &= &64& &~+~ &0 &~+~ &0 &~+~ &0 &~+~ &4 &~+~ &0 &~+~ &1\\ &= &69 \end{aligned}$$

That wasn't so hard, was it?

Let's try something a little tricker:

Example 2

Q. How would we represent the decimal number 1985 in binary?

A. If we know our powers of two this becomes easier:

$$\begin{aligned} 2^0 &= 1\\ 2^1 &= 2\\ 2^2 &= 4\\ 2^3 &= 8\\ 2^4 &= 16\\ 2^5 &= 32\\ 2^6 &= 64\\ 2^7 &= 128\\ 2^8 &= 256\\ 2^9 &= 512\\ 2^{10} &= 1024\\ 2^{11} &= 2048 \end{aligned}$$

Since we are only allowed to have either 0 or 1 of any of these powers of two, we can pick the unique combination of these powers we need to reach our number:

$$\begin{aligned} 1985 &= 1024 &+~& 512 &+~& 256 &+~& 128 &+~& 64 &+~& 1\\ &= {\textcolor{red} 1} \cdot 2^{10} &+~& {\textcolor{red} 1} \cdot 2^9 &+~& {\textcolor{red} 1} \cdot 2^8 &+~& {\textcolor{red} 1} \cdot 2^7 &+~& {\textcolor{red} 1} \cdot 2^6 &+~& {\textcolor{red} 1} \cdot 2^5 &+~& {\textcolor{red} 0} \cdot 2^4 &+~& {\textcolor{red} 0} \cdot 2^3 &+~& {\textcolor{red} 0} \cdot 2^2 &+~& {\textcolor{red} 0} \cdot 2^1 &+~& {\textcolor{red} 1} \cdot 2^0 \end{aligned}$$

So the binary representation of 1985 must be 11111100001

tip

Working with different number bases can get confusing, so there are a number of conventions to help make it clear which base we're working in.

For the rest of this discussion on number bases, and elsewhere in this book where it makes sense, we'll use the convention of putting a letter d after decimal numbers, like 1985d; and the number b after binary numbers, like 11111100001b. When we get to coding in assembly language, you might see us write binary number literals with a leading %, like %11111100001. In nearly all programming languages the default base is assumed to be decimal, so if you see something like 1985 in assembly language it's probably a decimal number.

Counting to sixteen in binary

Let's count from 0d to 16d in binary:

$$\begin{aligned} 0d &= 0000b\\ 1d &= 0001b\\ 2d &= 0010b\\ 3d &= 0011b\\ 4d &= 0100b\\ 5d &= 0101b\\ 6d &= 0110b\\ 7d &= 0111b\\ 8d &= 1000b\\ 9d &= 1001b\\ 10d &= 1010b\\ 11d &= 1011b\\ 12d &= 1100b\\ 13d &= 1101b\\ 14d &= 1110b\\ 15d &= 1111b \end{aligned}$$

What do we notice about the binary numbers?

1. The units ($2^0$) column alternates between 0 and 1. In fact, it's 0 for every even number and 1 for every odd number.
2. The second ($2^1$) column flips between 0 and 1 at half the rate of the units column, i.e. it goes 0, 0, 1, 1, etc.
3. The third ($2^2$) column flips between 0 and 1 at half the rate of the second column, i.e. it goes 0, 0, 0, 0, 1, 1, 1, 1, etc.
4. For every power of two (i.e. 0d = 0000b, 2d = 0010b, 4d = 0100b, 8d = 1000b), we observe that in binary the numbers always end in a string of 0s, and that they contain at most one 1 (except, of course) for 0d which has no 1s at all.
5. For every number before a power of two (i.e. 1d = 0001b, 3d = 0011b, 7d = 0111b, 15d = 1111b), we observe that in binary the numbers always end in a string of 1s.
6. If you look at any transition between 0 and 1 in a particular column, you'll see that the pattern of the columns to the right of it repeat. For example let's look more closely at what happens between 3d and 3d when the third column of the binary number ($2^2$) changes from 0 to 1:

$$\begin{aligned} 0d &= 00~~~{\textcolor{red}{00}}b\\ 1d &= 00~~~{\textcolor{red}{01}}b\\ 2d &= 00~~~{\textcolor{red}{10}}b\\ 3d &= 00~~~{\textcolor{red}{11}}b\\ \\ 4d &= 01~~~{\textcolor{red}{00}}b\\ 5d &= 01~~~{\textcolor{red}{01}}b\\ 6d &= 01~~~{\textcolor{red}{10}}b\\ 7d &= 01~~~{\textcolor{red}{11}}b\\ \end{aligned}$$

Do you see that the two right hand most do exactly the same thing both times, i.e. the sequence 00, 01, 10, 11? You can see the same thing happening when the fourth column ($2^3$) transitions from 0 to 1 between 7d and 8d also.

None of these observations are hugely surprising when we consider that the same things can be observed in decimal:

1. If a decimal number ends in a zero, like 10d or 50d or 2000d we know that it must be a multiple of ten, just as if a binary number ends in a zero, like 10b, 1110b or 101010b (corresponding to 2d, 14d and 42d respectively), we know that it must be a multiple of two, or what we call an even number.
2. Each column in decimal ticks up at a rate ten times slower than the column preceding it, just like in binary each column transitions twice as slowly as the one before.
3. Ditto.
4. The string of 0s at the end of powers of two in binary can be seen as the same effect as when, in decimal, we look at powers of ten, like 10d, 100d, 1000d, etc. They all end in zeros too.
5. Similarly, the strings of 1s at the end of binary numbers immediately preceding each power of two can be seen as equivalent to the observation numbers just before powers of ten in decimal will always end in a string of 9s, e.g. 9d, 99d, 999d, etc.
6. We can easily see the same repeated digit patterns in decimal as we see in binary when we consider that, for example, the unit column of decimal numbers always goes 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 over and over again. Similarly, if we counted from 0d to 1000d we'd notice that every time the third (hundreds) column ticked up by one, the numbers from 0d to 100d repeat in the first two columns.

Don't believe me? Try it out!

On both Windows and MacOS you should find that the built in calculator app will allow you to quickly convert from decimal to binary and back again to confirm all of the above. On other operating systems you may need to download calculator packages, or consult the documentation.

MacOS

The calculator on MacOS has three modes: Basic, Scientific and Programmer. You can switch to Programmer mode from the View menu, or by pressing ⌘ + 3. You can press `⌘ + 1 to go back to Basic mode.

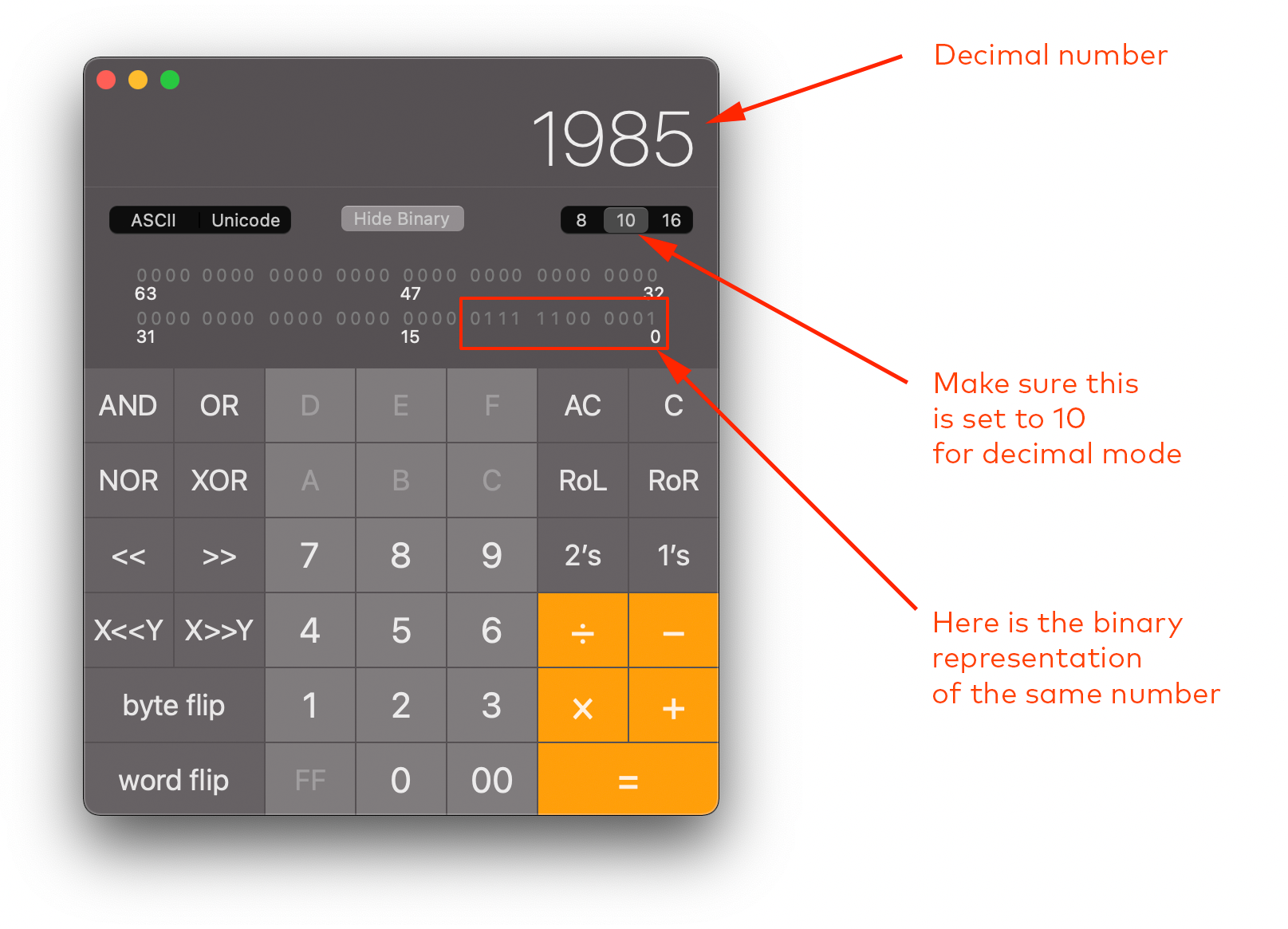
It might not be immediately obvious, but you are also able to click the binary digits (0s and 1s) in the binary section and it will flip the 0s to 1s and vice-versa, with a corresponding effect on the decimal number in the display.

tip

A really useful keyboard shortcut on this mode is that pressing the R key shifts between number bases, so if you accidentally find yourself in base 8 or base 16 (we'll explore these later!), you can get back to base 10 again.

Windows

WORK IN PROGRESS!

This page is not quite ready for visitors yet. Please check again another time.